Wat is meer: 3/4 of 5/6?
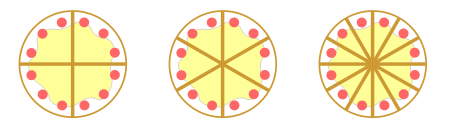
Je moet hier vierden en zesden met elkaar vergelijken. Dat gaat niet vanzelf. Maar met taarten los je veel problemen op. Hieronder zie je een taart die op drie verschillende manieren is gesneden. Links in 4 stukken, middenin in 6 stukken en rechts in 12 stukken.
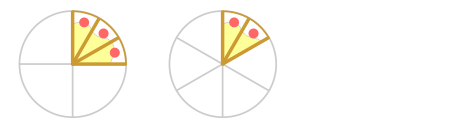
Je kunt hieronder goed zien dat 1/4 taart even groot is als 3/12.
Je ziet ook dat 1/6 taart even groot is als 2/12.
Je ziet ook dat 1/6 taart even groot is als 2/12.
Als je breuken met verschillende noemers (getallen onder de streep) met elkaar wilt vergelijken, moet je de breuken eerst zodanig omrekenen, dat ze dezelfde noemers hebben. Dit heet gelijknamig maken.
Gelijknamig maken
Als de noemers (het getal onder de streep) geen lastige getallen zijn, kun je vaak snel bepalen, naar welke noemer je de breuken moet omrekenen om ze gelijknamig te maken. Als je de "tafels" van deze noemers kent, weet je welke getallen in beide tafels voorkomen. Twee voorbeelden:
2/3 en 3/4 kun je omzetten naar twaalfden 8/12 en 9/12,
want 12 komt voor in de tafel van 3 (4x3=12) en de tafel van 4 (3x4=12).
1/8 en 5/6 kun je omzetten naar vierentwintigsten 3/24 en 20/24,
want 24 komt voor in de tafel van 8 (3x8=24) en de tafel van 6 (4x6=24).
2/3 en 3/4 kun je omzetten naar twaalfden 8/12 en 9/12,
want 12 komt voor in de tafel van 3 (4x3=12) en de tafel van 4 (3x4=12).
1/8 en 5/6 kun je omzetten naar vierentwintigsten 3/24 en 20/24,
want 24 komt voor in de tafel van 8 (3x8=24) en de tafel van 6 (4x6=24).
Terug naar de vraag waarmee dit verhaal begon.
Wat is meer: 3/4 of 5/6?
Je moet de breuken gelijknamig maken. In dit geval is 12 het handigste getal, want 12 komt voor in de tafel van 4 (3x4=12) en in de tafel van 6 (2x6=12).
Hoeveel twaalfden is 3/4? We hadden al gezien: 1/4 = 3/12.
3/4 is drie keer zoveel, dus 3/4 = 9/12.
Hoeveel twaalfden is 5/6? We hadden al gezien: 1/6 = 2/12.
5/6 is vijf keer zoveel, dus 5/6 = 10/12.
Wat is meer: 9/12 of 10/12?
Nu is het duidelijk: de tweede breuk bevat meer taart. Dus 5/6 is groter dan 3/4.
Je moet de breuken gelijknamig maken. In dit geval is 12 het handigste getal, want 12 komt voor in de tafel van 4 (3x4=12) en in de tafel van 6 (2x6=12).
Hoeveel twaalfden is 3/4? We hadden al gezien: 1/4 = 3/12.
3/4 is drie keer zoveel, dus 3/4 = 9/12.
Hoeveel twaalfden is 5/6? We hadden al gezien: 1/6 = 2/12.
5/6 is vijf keer zoveel, dus 5/6 = 10/12.
Wat is meer: 9/12 of 10/12?
Nu is het duidelijk: de tweede breuk bevat meer taart. Dus 5/6 is groter dan 3/4.
