Machtsverheffen is herhaald vermenigvuldigen.
Kwadraat
Het bekendste voorbeeld van machtsverheffen is het kwadraat, bijvoorbeeld 42 (spreek uit: vier kwadraat).
42 = 4 x 4 = 16
122 = 12 x 12 = 144
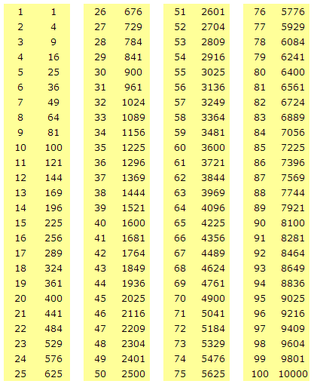
Hier volgt een overzicht van kwadraten t/m 1002 (dan hoef je die niet meer uit te rekenen):
Kwadraat
Het bekendste voorbeeld van machtsverheffen is het kwadraat, bijvoorbeeld 42 (spreek uit: vier kwadraat).
42 = 4 x 4 = 16
122 = 12 x 12 = 144
Hier volgt een overzicht van kwadraten t/m 1002 (dan hoef je die niet meer uit te rekenen):
Het verschil tussen kwadraten
Voor het uitrekenen van het verschil tussen twee kwadraten, kun je ook deze formule gebruiken:
162 - 122 = (16 + 12) x (16 - 12) = 28 x 4 = 112
Dat rekent misschien sneller dan:
162 - 122 = 256 - 144 = 112
Exponent groter dan 2
Het kleine hoger geschreven getal wordt exponent genoemd.
Als de exponent groter wordt, wordt de vermenigvuldiging vaker herhaald, bijvoorbeeld 2³ (uitgesproken als: "twee tot de derde" of "twee tot de derde macht" of "twee tot de macht drie").
2³ = 2 x 2 x 2 = 8
4³ = 4 x 4 x 4 = 64
2 tot de macht 10 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 1024
Exponent 0
De exponent is dus het aantal keren dat je het getal met zichzelf vermenigvuldigt. Maar hoe zit dat dan met "iets tot de macht nul"?
Kijk eens naar de volgende regelmaat:
3³ = 3 x 3 x 3 = 27
3² = 3 x 3 = 9
3 tot de macht 1 = 3 = 3
3 tot de macht 0 = ..............?
Telkens als de exponent 1 kleiner wordt, wordt de uitkomst in bovenstaand voorbeeld gedeeld door 3.
De laatste stap, van 3 tot de macht 1 naar 3 tot de macht 0 is dan ook weer een deling door 3. Dat levert het getal 1 als uitkomst op.
3 tot de macht 0 = 1
Dit geldt ook voor elk ander positief getal:
1 tot de macht 0 = 1
2 tot de macht 0 = 1
4 tot de macht 0 = 1
875 tot de macht 0 = 1
Negatieve exponent
En als je voortborduurt op bovenstaand rijtje, kun je ook beredeneren wat 3 tot de macht -1 en 3 tot de macht -2 zal betekenen.
3³ = 3 x 3 x 3 = 27
3² = 3 x 3 = 9
3 tot de macht 1 = 3
3 tot de macht 0 = 1
3 tot de macht -1 = 1 : 3 = 1/3
3 tot de macht -2 = 1/3 : 3 = 1/9
3 tot de macht -3 = 1/9 : 3 = 1/27
Voor het uitrekenen van het verschil tussen twee kwadraten, kun je ook deze formule gebruiken:
- a² - b² = (a + b) x (a - b)
162 - 122 = (16 + 12) x (16 - 12) = 28 x 4 = 112
Dat rekent misschien sneller dan:
162 - 122 = 256 - 144 = 112
Exponent groter dan 2
Het kleine hoger geschreven getal wordt exponent genoemd.
Als de exponent groter wordt, wordt de vermenigvuldiging vaker herhaald, bijvoorbeeld 2³ (uitgesproken als: "twee tot de derde" of "twee tot de derde macht" of "twee tot de macht drie").
2³ = 2 x 2 x 2 = 8
4³ = 4 x 4 x 4 = 64
2 tot de macht 10 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 1024
Exponent 0
De exponent is dus het aantal keren dat je het getal met zichzelf vermenigvuldigt. Maar hoe zit dat dan met "iets tot de macht nul"?
Kijk eens naar de volgende regelmaat:
3³ = 3 x 3 x 3 = 27
3² = 3 x 3 = 9
3 tot de macht 1 = 3 = 3
3 tot de macht 0 = ..............?
Telkens als de exponent 1 kleiner wordt, wordt de uitkomst in bovenstaand voorbeeld gedeeld door 3.
De laatste stap, van 3 tot de macht 1 naar 3 tot de macht 0 is dan ook weer een deling door 3. Dat levert het getal 1 als uitkomst op.
3 tot de macht 0 = 1
Dit geldt ook voor elk ander positief getal:
1 tot de macht 0 = 1
2 tot de macht 0 = 1
4 tot de macht 0 = 1
875 tot de macht 0 = 1
Negatieve exponent
En als je voortborduurt op bovenstaand rijtje, kun je ook beredeneren wat 3 tot de macht -1 en 3 tot de macht -2 zal betekenen.
3³ = 3 x 3 x 3 = 27
3² = 3 x 3 = 9
3 tot de macht 1 = 3
3 tot de macht 0 = 1
3 tot de macht -1 = 1 : 3 = 1/3
3 tot de macht -2 = 1/3 : 3 = 1/9
3 tot de macht -3 = 1/9 : 3 = 1/27
