|
De stelling van Pythagoras heeft te maken met rechthoekige driehoeken. Dat zijn driehoeken waarvan één hoek precies 90 graden is. Als je de lengte van de twee rechthoekszijden weet, kun je de lengte van de schuine zijde uitrekenen met de formule:
a2 + b2 = c2 |
|
|
De rechthoekszijden noemen we a en b, de schuine zijde is c.
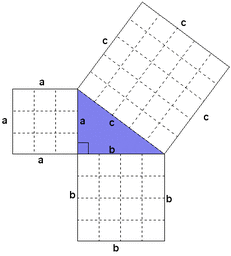
De schuine zijde wordt ook wel hypotenusa genoemd. Pythagoras heeft niet alleen gesteld dat volgens hem de formule zo is, maar hij heeft het ook bewezen. Er zijn op internet allerlei demonstraties en rekenvoorbeelden waarmee bewezen wordt dat a2 + b2 = c2. Een begrijpelijke uitleg die je met papier, liniaal en schaar zelf kunt nadoen, zie je op Wikipedia. |
Wie was Pythagoras?
|
Mooie combinaties
Bij de meeste combinaties van a en b wordt c een getal met cijfers achter de komma, maar er zijn ook combinaties van a en b waarbij de uitkomst c een geheel getal is.
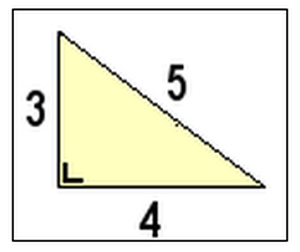
Bij de driehoek hieronder zijn a, b en c mooie ronde getallen: de rechthoekszijden (a & b) zijn 3 en 4 cm lang, de schuine zijde (c) blijkt precies 5 cm lang te zijn. Kijk maar:
Bij de meeste combinaties van a en b wordt c een getal met cijfers achter de komma, maar er zijn ook combinaties van a en b waarbij de uitkomst c een geheel getal is.
Bij de driehoek hieronder zijn a, b en c mooie ronde getallen: de rechthoekszijden (a & b) zijn 3 en 4 cm lang, de schuine zijde (c) blijkt precies 5 cm lang te zijn. Kijk maar:
|
|
3² + 4² = 9 + 16 = 25
De schuine zijde is dan de wortel van 25 en dat is 5, want 5² = 25.
Zie ook de pagina over worteltrekken.
Het is een kwestie van verhoudingen, dus wat voor de combinatie 3 en 4 geldt, geldt ook voor de combinatie 6 en 8:
6² + 8² = 36 + 64 = 100 = 102.
De schuine zijde is dan 10 cm.
De schuine zijde is dan de wortel van 25 en dat is 5, want 5² = 25.
Zie ook de pagina over worteltrekken.
Het is een kwestie van verhoudingen, dus wat voor de combinatie 3 en 4 geldt, geldt ook voor de combinatie 6 en 8:
6² + 8² = 36 + 64 = 100 = 102.
De schuine zijde is dan 10 cm.
|
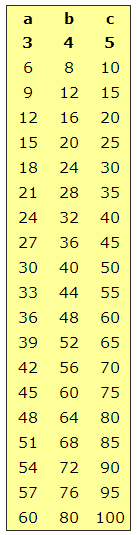
Zo kun je een heel rijtje maken waarvan de verhoudingen telkens 3:4:5 zijn:
|
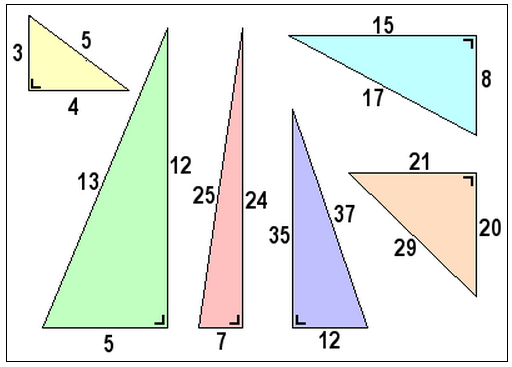
Maar er zijn meer combinaties waarbij a² + b² = c² mooie uitkomsten oplevert.
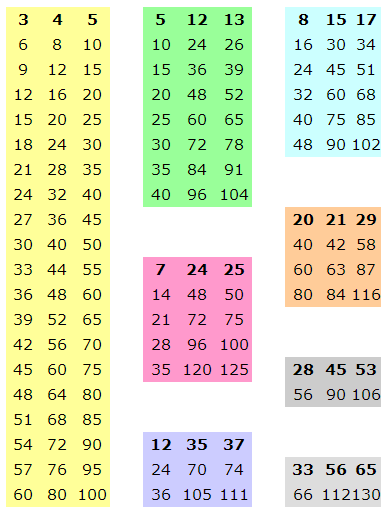
De driehoeken hieronder zijn onderling niet allemaal op dezelfde schaal getekend, maar de verhoudingen binnen elke driehoek zijn wel zoals de getallen aangeven. 3² + 4² = 9 + 16 = 25 = 52 5² + 12² = 25+ 144 = 169 = 132 7² + 24² = 49 + 576 = 625 = 252 12² + 35² = 144 + 1225 = 1369 = 372 8² + 15² = 64 + 225 = 289 = 172 20² + 21² = 400 + 441 = 841 = 292 
|
In de tabel hieronder staan deze verhoudingen nog eens, gevolgd door een of meer combinaties met dezelfde verhoudingen. De kleur komt overeen met de kleur uit de tekening hierboven.
